We have put forth a hypothesis that the brain bears the innate capability of performing high-level mathematical computing in order to perform certain cognitive tasks. We give examples of Orthogonalization and Fourier transformation and argue that the former may correspond to the physiological action the brain performs to compare incoming information and put them in categories, while the latter could be responsible for the holographic nature of the long-term memory, which is known to withstand trauma. We plead that this proposal may not be as strange as it may appear, and argue how this line of mathematical modeling can have far-reaching consequences.
How the brain processes information, where and how it stores them, and how it retrieves from memory as and when required, are some of the basic questions one is naturally curious about. In spite of neuroscience being an old discipline and the brain having been mapped extensively, one hardly knows much about the physiological mechanisms underlying such basic functions of the brain involving learning and memory. One has begun to develop some understanding on this account in the past few decades due to the efforts by psychologists (e.g. Donald Hebb [1]) and formal approaches by mathematicians, physicists, engineers, and cognitive scientists employing mathematical and cognitive models for certain brain functions. The theoretical approach not only gives crucial insight into how the brain functions, but also helps in designing and planning experiments that would otherwise be difficult and expensive, and in devising ways of processing and storing non-cognitive information. The latter may pertain to information technology. It is our contention that the mathematical and cognitive models of brain processes should give ideas to construct algorithms to handle numerous non-cognitive problems.
In this short communication, we summarize one such theoretical approach we have pursued for some time. We have hypothesized since 2000 [2] that in many situations the brain might be functioning in a mathematical manner in that it might be using mathematical functions and transformations (which are otherwise well known to mathematicians and physicists) to perform certain cognitive tasks. A natural question that will arise then is “how would an untrained brain know about these functions and transformations?” To this end, we go on to conjecture that the brain might be hard-wired to do such mathematical functions and transformations, and that these competencies might have been acquired by the brain in the course of evolution while mathematicians and physicists have been only reinventing them. Apparently, a section of modern philosophers also believes so.
Let us start with the basic question: how do we learn? — On the basis of certain experimental observations, a psychologist Donald Hebb [1] put forth a hypothesis that the synaptic efficacies, i.e. the nature (whether excitatory or inhibitory) and strength of synaptic connections between numerous neurons in the brain, change as and when an information is registered. The synapses have plastic character, i.e. the modification in their efficacies stay, sometimes for short durations and sometimes over longer periods, and it is through this ongoing process of modifications that we learn and store information in synapses.
Electrical impulses are constantly exchanged by the huge number of neurons (≈1011) when the brain is active. Suppose, when information comes to be recorded, the neurons are already individually potentiated (or inhibited) to certain levels, which may be a base level or a level reached in the course of assimilating earlier information. The level of potentiation or inhibition will typically vary from one neuron to the other. The new information triggers them and some of them that might have been already near the threshold of firing might fire, i.e. send out electrical impulses, while the others remain quiescent. These impulses are received by other neurons via synapses, which, depending on their chemical character, whether excitatory or inhibitory, will excite or depress the neurons that are the recipients of the impulses. A neuron receives such excitatory and inhibitory inputs from a large number of pre-synaptic neurons and adds them linearly. If the net effect of the combined input makes the recipient neuron cross its threshold, which is pre-assigned to it by nature, then it fires an electrical impulse that is received by a large number of neurons via synapses. Note that the signal or impulse sent out by a neuron is replicated into as many of them as the number of neurons this particular neuron is synaptically connected with.
Thus, we see that the neurons might be already programmed to add linearly. The brain also knows how to multiply as an input from a pre-synaptic neuron goes to a post-synaptic neuron weighted by the synaptic efficacy of the synapse connecting them. The combined capabilities of neurons to add, and the neuron-synapse duos to multiply enable the neuronal network to form memories and the Hebbian plasticity enables them to be stored in the synapses. We further propose that when these competencies are extended over a collection of neurons and synapses, they enable them to also perform mathematical operations of higher levels like ‘orthogonalization’ and ‘Fourier transformation’. We have studied these two mathematical operations, in particular, to propose that the brain might employ them respectively to discriminate between information [2,3] and make the long-term memory robust against trauma [4]. When we categorize information, we compare entities and isolate similarities and differences between them. To acquire this capability, we argue, the brain employs the mathematics involved in orthogonalization. Orthogonalization is a mathematical transformation that converts a given set of vectors into a set of mutually perpendicular or orthogonal vectors. So how is it connected with the brain and its capability to discriminate between information to categorize them? To address this question, we will first prepare the background.
As mentioned above, 1011 odd neurons are all the time busy exchanging electrical impulses or ‘action potentials’ via approximately 1015 synaptic connections, which are either excitatory or inhibitory in nature and can have a range of values for their strengths. In this dynamical scenario, when information comes to be recorded, it triggers the neural activities, as a result of which some neurons fire while others are unable to. This pattern of firing and quiescent neurons is taken to correspond to the incoming information. And, in this picture, in which the information is spread out over a large network of neurons and synapses, an information is represented by an N-dimensional vector whose N components are +1 or –1, where +1 represents a firing neuron and –1 represents a quiescent neuron. Thus, an information, which can be an object, a smell or anything perceived through the sense organs, is designated by an N-dimensional vector, say = {+1,–1,–1,+1,–1,+1,+1,–1,–1,...}. The N components in a network of N neurons represent features of the object, while +1 or –1 indicates yes or no for a feature to be found. How the vector
is stored in the network of neurons and synapses was prescribed by Hebb, who observed that the strength of a synapse depends on the activities of the neurons on either end of it. For instance, if both the neurons are active, then the synapse can become stronger than when one is active and the other is not. Even when both the neurons are inactive, the synapse can be construed as becoming stronger in a relative sense.
Mathematically, we can represent the Hebbian rule as
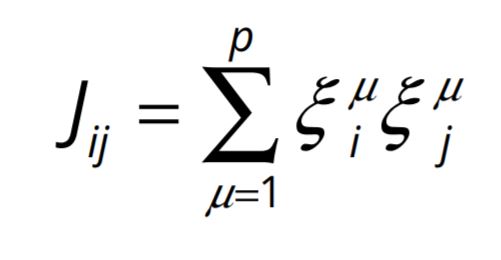
(1)
Here represents the i th component of the vector
, i.e. activity on the i th neuron of the μ th input pattern. The J ij represents the strength of the synapse between neurons i and j and it depends on the activities on neurons i and j in the pattern μ . Note that, as Hebb’s hypothesis postulated, the J ij changes cumulatively every time a new pattern μ is inscribed.
A highly connected network of binary neurons undergoing interaction of the type in eqn. (1) can be represented by the following Hamiltonian, or total energy function.
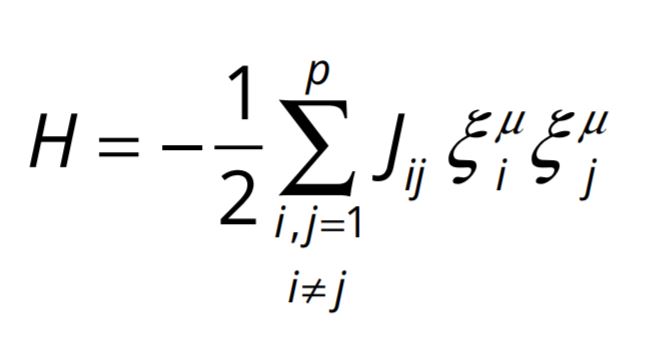
(2)
The minima of this Hamiltonian will represent stable states of the network. In representing our network by this Hamiltonian, we have taken our cue from the physics system called spin glass [5], in which the magnetic atoms having spins either up or down interact in a manner similar to eqn. (1) over all ranges of separation and the system settles down in an exponentially large number of stable or minimum energy states, each being a random configuration of up and down spins.
This model offers a useful scenario and a mathematical framework that can be adapted to model memory – each pattern of up and down spins that minimizes the Hamiltonian can be visualized as a memory of an entity represented by a pattern (or array) of firing and non-firing neurons.
This model of memory originally conceived by Hopfield [6] gives useful insight into the working of memory as a stable state of the model brain, but it suffers from a serious constraint — if the number of stored memories exceeds 0.14 × N, N being the number of neurons in the brain, then a memory blackout begins to set in, i.e. retrieval from memory deteriorates rapidly and soon nothing that is stored in the synapses can be recalled [7-9].
The prescription for retrieval/recall is
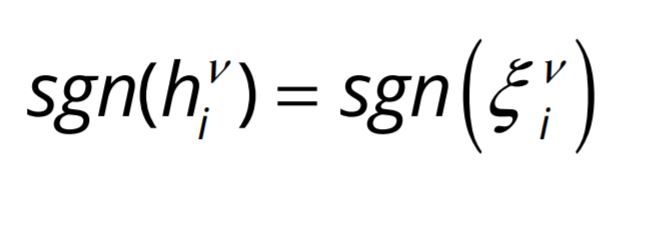
(3)
where the symbol ‘sgn’ represents the sign of or
, and
gives the local field potential on neuron i in the pattern ν , which is a combined result of projections of activities on all the neurons on to the neuron i ; each projection from a neuron is weighted with the efficacy J ij of the synapse connecting that neuron with i . This is given by
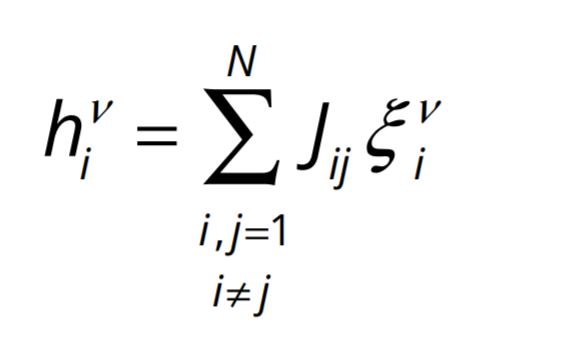
(4)
If the condition (3) is satisfied for a pattern , then we consider the latter to be retrieved. We can then say that
is one of the memories stored by the network.
While 0.14*N is quite large, since N is of the order of 1011, what is unrealistic about the blackout is that the model brain breaks down when it is overloaded. The reason for this shortcoming is simple to understand. Even though the patterns being stored as memories are generated randomly, they inevitably have non-zero overlaps between themselves, i.e. the dot-product between any two vectors, s, will be non-zero. This leads to noise due to cross-talks (in eqn. (4)) between
, which is presented for retrieval from memory, and all the other
s stored in the memory. This can be seen easily by substituting for J ij from eqn. (1) and expanding the summation in eqn. (4). The noise builds up as more and more vectors are lodged in the memory, and at one stage the signal,
, submerges in the noise, and retrieval, as per eqns. (3) and (4), becomes impossible.
It should be noted that in order to categorize or classify information, we need to search for similarities among the given entities. That is, their vectors should actually overlap with each other. But, then, as we have seen above, that would lead to the serious problem of memory blackout. So, how do we resolve this dichotomy?
We have proposed that before lodging in the memory, the brain can orthogonalize the vector corresponding to incoming information with respect to all the vectors in the memory store [2]. Orthogonalization is a mathematical transformation that converts a given set of (linearly independent) vectors into a set of mutually perpendicular vectors [10]. It is our hypothesis that the brain stores in the synapses (in the usual Hebbian manner, as in eqn. (1)) the orthogonalized vectors rather than the original or the raw vectors s. This drastically new hypothesis enables the brain to store ‘similarities’ and ‘differences’ of the new incoming information with those in the memory store rather than the full information contained in the incoming vector [11].
The orthogonalization strategy also provides the system with some economy on storage [2]. For instance, if we consider two objects (only for simplicity), one is stored and the second one has been orthogonalized with respect to the first to prepare it to be imprinted, we will find that similarities are stored with greater emphasis (or weight) in case the two objects are very different from each other; on the other hand, if the two objects happen to be very similar, then the model brain will store the similarities with smaller amplitude than the differences between them, which we find are fewer in number. We can say that this model brain has an additional and cognitively appealing capability of paying greater attention to similarities in very different objects and to differences in very similar objects – i.e. greater attention is paid to whichever is lesser between similarities and differences.
While the immediate effect of orthogonalization is that the noise is eliminated and consequently the memory capacity jumps from 0.14 N to N, but more importantly, as a big bonus, we find that the orthogonalization bestows the model brain with significant cognitive capabilities explained above, besides providing it with a built-in feature of economy, which is generally ubiquitous in nature [2,3].
The neuronal network we have described also has the feature of content addressability. It can retrieve an inscribed when presented with something similar to it, that is, the network can ‘associate’ other patterns (outside the set of learnt ones) with those in the stored memories and recall the latter individually. In fact, the imprinted or learnt patterns act as attractors, and associated with each imprinted pattern there is a basin of attraction. An arbitrarily chosen pattern in a basin of attraction, if presented for association, will converge to the attractor, which is at the bottom of the basin. We can treat the set of patterns inside a basin of attraction as belonging to a group or category with the attractor at the bottom of the basin being the representative of the group. Alternatively, we can say that the network acts as an error corrector – patterns inside a basin differ from the imprinted pattern or the attractor on a few sites; if we view the mismatches as errors, then the convergence of such erroneous patterns to the imprinted pattern on presentation for retrieval would amount to error correction.
We are investigating a number of issues related with basin of attraction and stability of memories with and without orthogonalization that are of relevance to cognition. This work is currently in progress and should be ready for publication quite soon.
We are also investigating the use of orthogonalization schemes due to Löwdin [12-14]that are very different from that of Gram-Schmidt and have the potential of giving insight into forms of memories other than the associative memory. The Gram-Schmidt scheme orthogonalizes in a sequential manner, which is relevant to the processes like learning of languages. On the other hand, the Löwdin schemes are democratic in nature, because they take all vectors and orthogonalize them all together in one go. As new vectors are added, the entire lot of orthogonalized set gets modified. They are thus expected to help us understand episodal and semantic memories. In a preliminary study, we have also found that the orthogonalization schemes help us in addressing questions pertaining to lodging of words in mental lexicon and their retrieval. For instance, we have attempted a study on the age-old problem in grammar – whether words are stored in their full glory or as word parts.
We have also studied another vital question pertaining to a common observation that due to an accident or due to ageing we may lose shortterm memories, but almost always we retain old memories, i.e. long-term memory is robust against trauma and ageing, which involve destruction or decay of neurons and synapses. We have proposed that the long-term memory may have a holographic character so that even if a part of the constituent units is destroyed or obfuscated, the surviving units can put together the whole memory like in the case of an image of a hologram. In mathematical terms, this would imply that the brain might possess the ability to Fourier transform the information when sending the memories formed in Hippocampus to the long-term memory areas in Cortex. We have adapted Fourier transformation into our model for learning and memory and demonstrated how full memories can be constructed even if some synapses, and along with them some neurons, are destroyed (see ref. [4] for full discussion).
The above results are indeed derived from rigorous calculations, mathematical as well as computational, the details of which are not given here but can be found in references [2-4,11]. In order to drive home a particular point to a mixed readership of wide cross-section, we have kept the description largely to a qualitative level by minimizing on mathematical expressions. We are working together with experimentalists to substantiate our hypotheses and conjectures through experiments. We are beginning to find favorable evidences. This work is currently in progress in collaboration with Dr. DJ Parker at Cambridge University.
The ideas and hypotheses expressed here are in initial stages of development. A lot of work, including experimental, needs to go in before the hypotheses become theories to explain the mechanisms of certain cognitive functions. It should be appreciated that the ideas and mathematical frameworks developed in one particular branch of science can be useful to understand the phenomena happening in another completely unrelated area of science. The present set of works highlights one such example.
Our discussion is more or less in generic terms without reference to any particular area of the brain. However, adaptation to any specific part of the brain engaged in a specific task may not be a problem. In a broad sense, we know that the neuronal networks in different parts of the brain process different types of information and that many of these networks may be interacting with each other. The nature of long-range interactions, for instance the special kind in spin-glasses [5], can give insights into the interactions between the networks and in turn help in understanding the functional networks that are typically revealed in functional imaging [15,16]. Application of the orthogonalization, particularly Löwdin’s ‘canonical’ [10,14], can give the intensity or magnitude of activities in the various connected networks in a graded manner.
Finally, it is being recognized that glial cells play a role in memory formation [17]. We have not touched up on it as yet, but it should be interesting and instructive to integrate glial cells with the attractor neuroal networks. This will involve a lot of out-of-the-box thinking and throw up major challenges to theoretical neuroscientists. It must be appreciated that the discipline of theoretical or formal neuroscience calls for collaboration between experts trained to do neurosciences, including experimentalists, on one hand, and formal scientists like physicists and computer scientists on the other.
Received date: September 29, 2017
Accepted date: December 01, 2017
Published date: May 28, 2018
None
None
VS would like to express gratitude for (late) Sir Sam Edwards and Dr David J Parker for collaborating on some of these out of the ordinary ideas. Thanks are due to the Leverhulme Foundation (UK) and the Royal Society (UK) for financial support, and to Cavendish Laboratory and the Department of Physiology, Development and Neuroscience, University of Cambridge (UK) for providing infrastructure to carry out some of these works.
© 2018 The Author (s). This is an open-access article distributed under the terms of the Creative Commons Attribution 4.0 International License (CC-BY).
Constraint-induced music therapy (CIMT) has been shown to enhance hearing recovery in patients with sudden sensorineural hearing loss (SSNHL) by preventing maladaptive reorganization of the auditory cortex. This study was the second research to provide scientific evidence related to the neuroplasticity of the central auditory nervous system in response to constraint-induced acoustic rehabilitation.
Srivastava V, Sampath S. Could the brain function mathematically? Neurol Neurosci Res 2018;1(1):4. https://doi.org/10.24983/scitemed.nnr.2018.00064